In China, there is a popular nursery rhyme: Once upon a time there was a mountain, in which there was a temple, in which there was an old monk telling a story to a little monk. The story he was telling is: Once upon a time there was a mountain, in which there was a temple, in which there was an old monk telling a story to a little monk…… It continues endlessly until the child falls asleep. This rhyme is a typical manifestation of the concept of self-similarity.
In mathematics, self-similarity describes the property of an object if a part of it resembles the whole object. In the aforementioned nursery rhyme, the story the old monk tells is the same as the rhyme itself. There are lots of instances of self-similarity in nature, such as Romanesco Broccoli, the fern leaves, the top of trees, and coastlines, all appearing self-similar approximately.

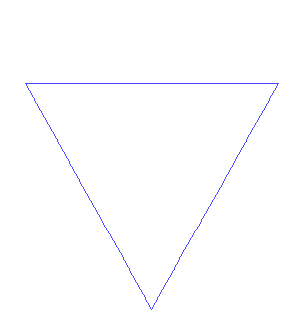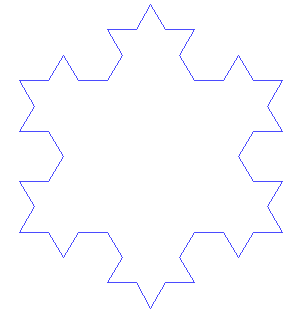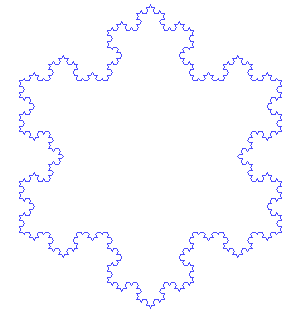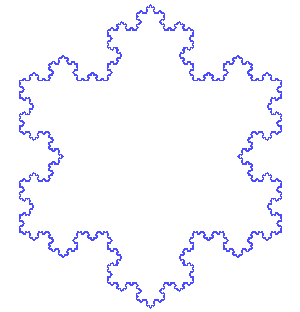
Self-similarity is a significant property of fractals, with a famous representative being the Koch snowflake. To construct the snowflake, start from an equilateral triangle, and replace the middle 1/3 of each side by a smaller equilateral triangle without base, pointing outwards. The final shape is achieved by repeating the above step for every side of the resulting shape infinitely. If we focus on one petal of the Koch snowflake, the so-called Koch curve, and magnify it 3 times again and again, it always turns out exactly similar to the original curve. The most interesting feature of such a fractal is, being a closed shape it has a finite area (8/5 times the original equilateral triangle’s area), but its perimeter is infinite! Each of the iteration enlarges the perimeter by a factor of 4/3, and thus the perimeter diverges as the iteration repeats forever.

Having various magical mathematical properties, how does self-similarity play a role in modelling physical phenomena? In physics there are numerous similar phenomena occurring in systems with different scales in size, mass, energy etc. In particular for the concerns of our group, relativistic jets exist in systems accross roughly eight orders of magnitude in mass, from stellar scale XRB to galactic scale AGN. The similar observational features of jets in XRB and AGN makes us believe they have similar origins, both from the accretion onto a central compact object. Such a physical mechanism must be scaling invariant, with the dimensional quantities (length, accretion rate etc.) varying while the dimensionless quantities (angle, accretion efficiency etc.) remaining similar. This requires the physical quantities being expressed as power-laws of the geometrical quantities, and thus their dependence on each of the coordinates can be separated. As a result, the assumption of self-similarity reduces the number of independent variables, and simplifies the problem by turning partial differential equations into ordinary differential equations, allowing analytical or semi-analytical solutions.
In our current project on jet launching, we assume stationary, axisymmetric MHD flows with radial self-similarity, i.e., the flow quantities scale with the cylindrical distance to the rotation axis. Based upon these assumptions, we try to derive the general relativistic MHD equations, and compare with the special relativistic version obtained in previous studies.